The Theory of Quantum Matter group led by Dganit Meidan is part of the condensed matter theory group of the physics department at Ben Gurion University of the Negev. Information on open positions can be found here.
Our group is interested in systems where quantum mechanics gives rise to fascinating physical properties. Our main area of research is topological matter with a focus on topological superconductors, topological semi-metals, interacting topological phases and topological pumps. In particular we are interested in the way interactions affect the physical properties of the emergent end states, and the way these changes manifest themselves in experimentally measurable quantities.
Prof. Dganit Meidan

Department of Physics
Office: Building 54, Room 226
Ben-Gurion University of the Negev
Beer Sheva 84105, Israel
Email: dganit@bgu.ac.il
Phone: +972 (0)8 6461170
Join Our Group!
Our group is looking for talented postdocs, PhD, and Master students.
Highlights
Measurement induced topological transition
We study a free fermion model where two sets of non-commuting continuous measurements induce a transition between area-law entanglement scaling phases of distinct topological order. The continuous nature of the measurement, allows us to introduce a “partial post-selection mapping” to a parent non-Hermitian Hamiltonian. Using this mapping we can uniquely associates topological invariants to the topological phases of the non-unitary stochastic dynamics.
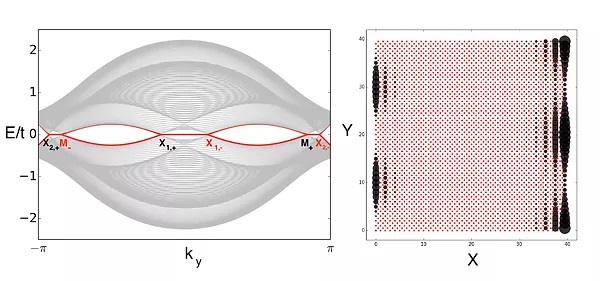
Josephson current phase relation of nodal superconductors
We propose the use of Josephson current as a probe for identifying the nodal superconducting phase. Topological superconductors are known to have a signature 4π periodic current phase relation unlike the 2π periodicity associated with conventional superconducting states. We show that the nodal superconducting phase has a tunable current-phase relation which is controlled by the momentum transverse to the current across the junction. This feature is unique to nodal topological superconducting phases and allows to unambiguously establish its presence. We interpret these results as arising from a transition between a trivial and two distinct topological phases associated with different winding numbers.
R. Seshadri, M. Khodas and D. Meidan, arXiv:2201.11514
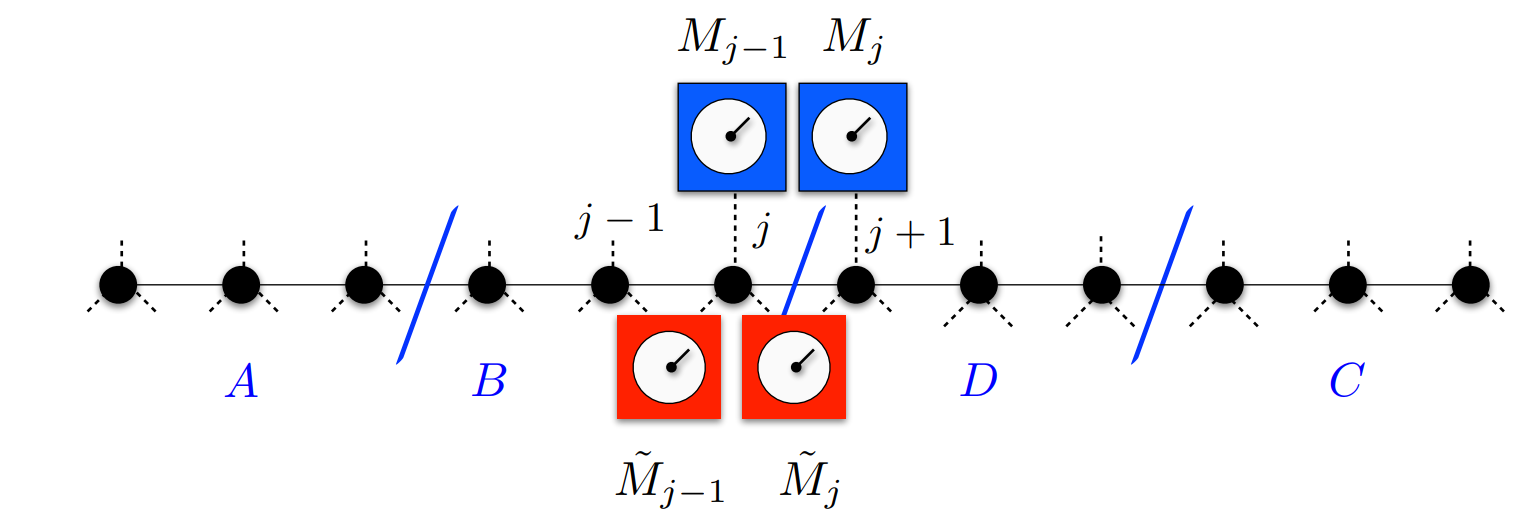
Localization enhanced and degraded stability of zero modes
The prospects of building quantum devices based on topologically ordered states of matter has caused a great deal of excitement. An important recent conjecture suggests that topological features in interacting Majorana wires can be enhanced with additional protection due to disorder-induced localization. This notion has been called localization-protected topological-order and its consequences could be far-reaching, allowing for quantum processors based on topological superconductors to be operated at high temperatures. Although this would be a remarkable feature, proposals for localization-protected topological-order have been met with some scepticism as both disorder and interactions are known to destroy the topological gap that protects the zero modes. More crucially, the lack of direct numerical evidence to support this conjecture has hindered its acceptance.
Together with our colleagues Graham Kells and Niall Moran we study the stability of the many body zero modes in the presence of interactions and disorder. Our analysis identified two regimes in which disorder exhibits opposing effects on the stability of the zero modes. In particular, we identify a regime of parameters where many body effects dominates, and disorder reduces the multi-particle content of the zero mode, which in tern enhances the stability of the zero modes. These results allow to identify optimal experimental conditions to perform Majorana manipulations, and quantum information processing.
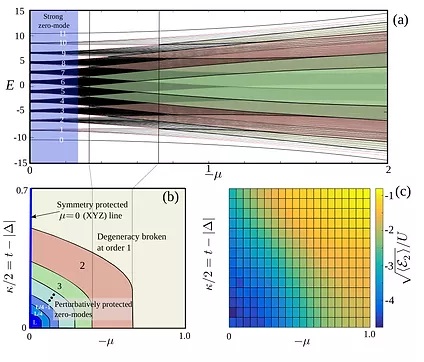
S. Nulty, J. Vala, D. Meidan, and G. Kells, Phys. Rev. B 102, 054508 (2020)
G. Kells, N. Moran, and D. Meidan, Phys. Rev. B 97, 085425 (2018)
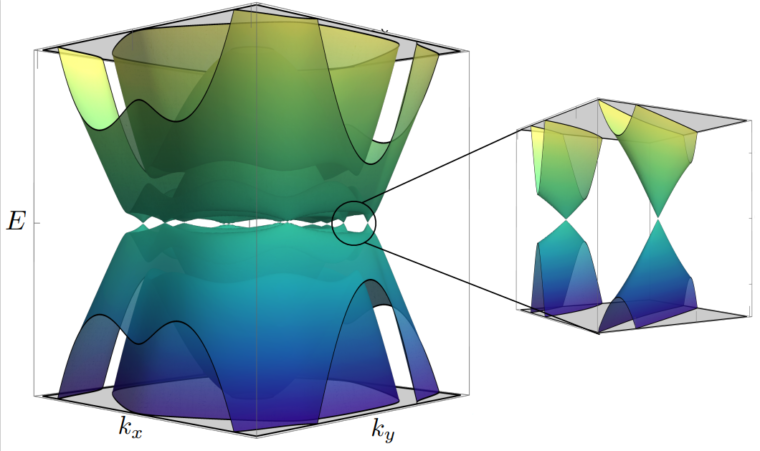
Edge states in topological semi-metals
Weyl semimetals are characterized by a band structure, where valence and conduction band touch at discrete isolated points in the Brillouin zone. One of the striking features of the Weyl semimetals is an emergence of the Fermi arc that are robust against the disorder and a surface preparation.
Unlike in three dimensional materials where these Weyl nodes are stable to any (sufficiently weak) perturbation, robust Weyl semimetals in two dimension do not exist. The closest analog was recently proposed by Young and Kane, who considered two-dimensional lattice with non-symmorphic symmetries. They show that by breaking of time reversal or inversion symmetry one can split the Dirac cones into Weyl node. We found that this splitting is accompanied by the formation of gapless edge states. The type and strength of applied deformation control the location and Weyl nodes and the composition of the respective edge states. This sensitivity to the external deformations makes non-symmorphic materials potentially useful as a new type of electromechanical sensors.
P. G. Matveeva, D. N. Aristov, D. Meidan, and D. B. Gutman, Phys. Rev. B 99, 075409 (2019)
Heat pumping from braiding Majorana zero modes
Following the first wave of experiments designed to detect Majorana bound states, the next generation of experiments and theoretical proposals aim at probing directly their non-local topological properties, with the ultimate goal of optimising and controlling their manipulation.
In a recent work we study the transport signatures of a braiding protocol of Majorana zero modes in a Y-junction layout. We show that the heat pumped during the braiding cycle is a universal quantity, independent of the details of the driving and of the couplings to the external leads. This universal value stems directly from the geometric properties of the braiding cycle in parameter space. Our results can be used for better experimental control of the exchange process and can provide a new potential tool for engineering heat pumping device.
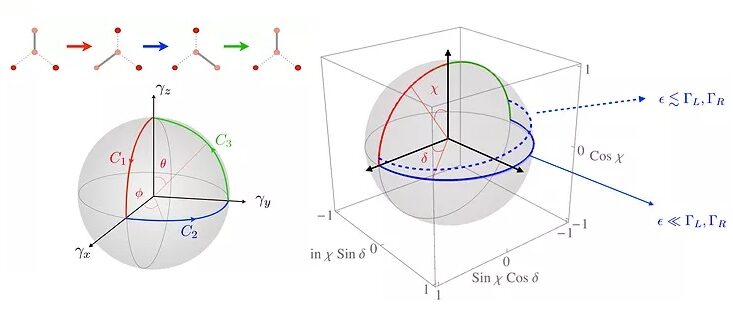
Dganit Meidan, Tal Gur, and Alessandro Romito, Phys. Rev. B 99, 205101 (2019)
Thomas Simons, Dganit Meidan, and Alessandro Romito, Phys. Rev. B 102, 245420 (2020)