Schechter's research group
Welcome to my homepage!
My group is part of the Condensed Matter Theory Group in BGU’s Department of Physics. My research interests include disordered and amorphous solids, glasses, decoherence and relaxation in superconducting qubits and resonators, quantum magnetism, disordered magnets. I am currently seeking MSc and PhD students to fill several positions.

Recent Research Topics
Quantum defects in amorphous solids and coherence and relaxation of superconducting qubits and resonators
Low temperature universality and the two-TLS model
A large variety of otherwise very different amorphous and disordered solids show, at temperatures lower than 3 Kelvin, remarkable universality in their properties. Most astounding, the ratio λ/l of the phonon wavelength divided by its mean free path is roughly 1/150, this value being constant in wavelength, temperature, and very similar between otherwise very different materials.
For 5 decades this phenomenon is discussed within the framework of the phenomenological model of tunneling two level systems (TLSs). However, crucial questions such as the nature of the tunneling states, the universality and smallness of the ratio λ/l, and the energy scale dictating the temperature of 3K below which the phenomenon is observed, have remained unanswered.
At the same time, since 2005 it is recognized that these TLSs, which are generic to bulk amorphous solids and to surfaces, are the dominant source of noise, decoherence, and relaxation in many quantum devices, including superconducting qubits and resonators.
Our research is dedicated towards the understanding of the nature of the TLSs and the physics behind the low temperature universality of amorphous solids, and at the same time towards better understanding of the deleterious effects TLSs have on quantum devices, and of ways to diminish these effects, towards enhanced efficiency and stability of quantum circuits.
Central to our research is a generalized model for the TLSs we suggested a decade ago. Within this model two types of TLSs exist, differing by the strength of their interaction with the strain. The model is rigorously based on tunnelling defects in disordered crystals, see e.g. in:
- A. Gaita-Arino and M. Schechter, Identification of Strong and Weak Interacting Two-Level Systems in KBr:CN. Physical Review Letters 107, 105504 (2011).
- M. Schechter and P. C. E. Stamp, Inversion symmetric two-level systems and the low-temperature universality in disordered solids. Physical Review B 88, 174202 (2013).
- A. Churkin, D. Barash, and M. Schechter, Nonhomogeneity of the density of states of tunneling two-level systems at low energies. Physical Review B, 104202 (2014).
- A. Churkin, I. Gabdank, A. L. Burin, and M. Schechter, The strain gap in a system of weakly and strongly interacting two-level systems. The European Physical Journal: Special Topics 232, 3483 (2023).
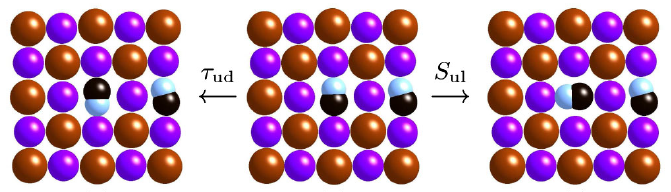
Weakly interacting (flip, tau) TLS, and strongly interacting (rotation, S) TLS of CN impurities in KBr. From Gaita-Arino and Schechter (2011).
Recently, the assertion that the two-TLS model applies also to amorphous solids received strong experimental support in observed excess loss of superconducting resonators in far from equilibrium conditions. Some other phenomena in which the strongly interacting TLSs are dominant, and thus the two-TLS model gives distinct predictions from the STM are the Ramsey and Echo decay rates of TLSs as function of applied strain, and the spectral mixing of TLS under thermal cycling. Effects of the strongly interacting TLSs on the response of qubits and resonators and on the stability of superconducting quantum circuits is a central research direction in our group. Some of our current interests are the frequency shift of superconducting resonators induced by biasing the TLS bath, and the effect of the strongly interacting TLSs on this frequency shift.
- S. Matityahu, A. Shnirman, Gerd Schon, and M. Schechter, Decoherence of a quantum two-level system by spectral diffusion. Physical Review B 93, 134208 (2016).
- M. Schechter, P. Nalbach, and A. L. Burin, Nonuniversality and strongly interacting two-level systems in glasses at low temperatures. New Journal of Physics 20, 063048 (2018).
- L. Yu et. al, Experimentally revealing anomalously large dipoles in the dielectric of a quantum circuit, Scientific Reports 12, 16960 (2022).
- A. L. Burin, M. Schechter, D. Tennant, Y.J. Rosen, Red shift of the superconductivity cavity resonance in Josephson junction qubits as a direct signature of TLS population inversion. arXiv:2401.15624, (2024).
- Y. Reiss and M. Schechter, Thermal cycling – evidence for a generalized tunneling model and a tool to distinguish noise sources in quantum circuits. arXiv:2410.19930 (2024).
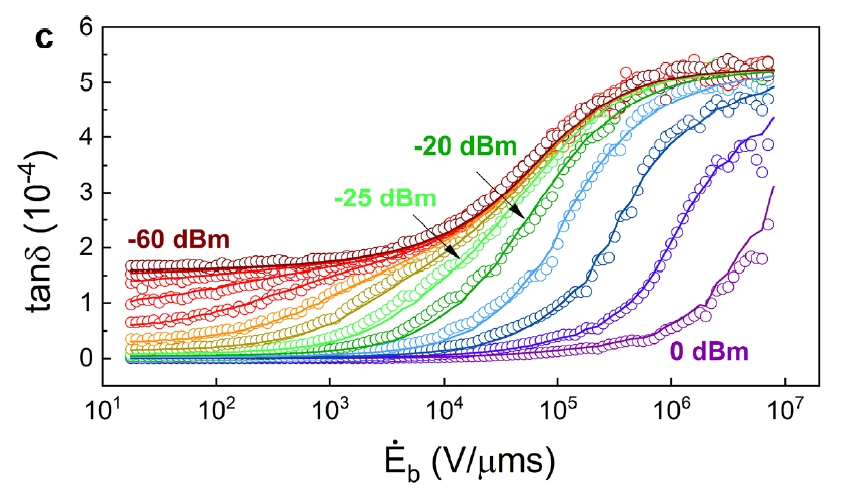
Excess loss due to strongly interacting TLSs. From Yu et. al. (2022).
Improving coherence and scalability of quantum circuits
Another facet of the research of the interactions between the TLSs and superconducting qubits and resonators is the possibility to diminish the deleterious effects of TLSs on quantum devices. Recently we have shown that periodic biasing of the TLS bath can reduce loss in driven superconducting resonators, can reduce fluctuations in relaxation times in superconducting qubits, and can reduce the mean dephasing time in superconducting qubits.
- S. Matityahu, H. Schmidt, A. Bilmes, A. Shnirman, G. Weiss, A. Ustinov, M. Schechter, and J. Lisenfeld, Dynamical Decoupling of Quantum Two-Level Systems by Coherent Multiple Landau–Zener Transitions. Quantum Information 5, 114 (2019).
- S. Matityahu, A. Shnirman, M. Schechter, Stabilization of Qubit Relaxation Rates by Frequency Modulation. Physical Review Applied 16, 044036 (2021).
- S. Matityahu, A. Shnirman, M. Schechter, Qubit dephasing by spectrally diffusing quantum two-level systems. Physical Review Applied 21, 044055 (2024).
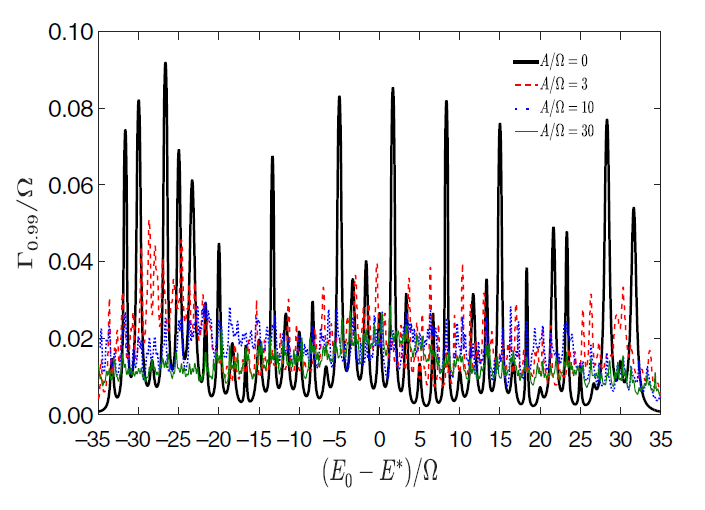
Reduction of fluctuations in the relaxation rate of qubits, from Matityahu et. al. (2021).
Quantum disordered magnets
The interest in magnetism, and specifically quantum magnetism, is twofold. Firstly, magnetic materials are of immense significance for the advance of technology. With reduced size of current and future devices, quantum effects become relevant, and their understanding is crucial to further advance. At the same time, magnetic systems are an ideal tool in the study of various physical phenomena, as they allow the realization of theoretical models with negligible extraneous interactions, and with the ability to tune the relevant parameters.
Perhaps the most studied model for interacting systems is the Ising model. With the addition of a transverse field term and a random field term the model allows the study of the interplay of interactions, quantum fluctuations, and disorder. This model is experimentally realized in anisotropic dipolar magnets in transverse field. We have thoroughly studied theoretically the phase diagram of such systems, pure and disordered, in their ferromagnetic and glass phases, and in mixed Ising – XY magnets.
- J. C. Andresen, C. K. Thomas, H. G. Katzgraber, and M. Schechter, Novel Disordering Mechanism in Ferromagnetic Systems with Competing Interactions. Physical Review Letters 111, 177202 (2013).
- J. C. Andresen, H. G. Katzgraber, and M. Schechter, Random-field-induced disordering mechanism in a disordered ferromagnet: Between the Imry-Ma and the standard disordering mechanism. Physical Review B 96, 214414 (2017).
- T. Dollberg, J. C. Andresen, and M. Schechter, Effect of intrinsic quantum fluctuations on the phase diagram of anisotropic dipolar magnets. Physical Review B Letters 105, L180413 (2022).
- T. Dollberg and M. Schechter, LiHoF4 as a spin-half non-standard quantum Ising system. SciPost Physics 17, 028 (2024).
- T. Dollberg and M. Schechter, Off-diagonal dipolar interactions in a mixed Ising–XY magnet: the case of LiHoxEr1-xF4. In preparation.
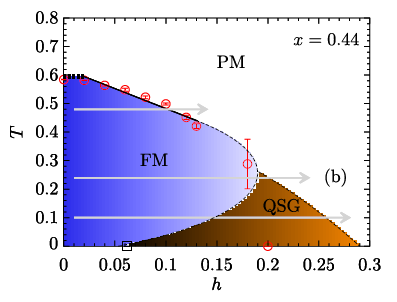
Ferromagnet to glass quantum phase transition, from Andresen et. al., (2013).
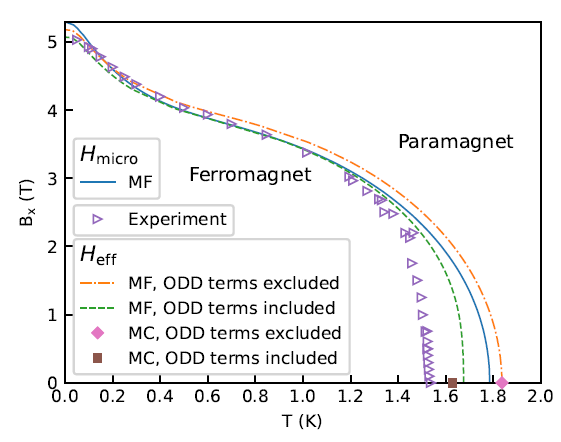
Phase diagram of LiHoF4, from Dollberg and M.S. (2023).
Thermodynamic phases and dynamical properties of glasses
Glassy dynamics, including phenomena such as slow relaxation and memory, are common to a wide variety of disordered and frustrated systems. Some of these systems, for example spin glasses, also show a thermodynamic phase transition to a low temperature glass phase, having long range glass order. Other systems, for example structural glasses, show a crossover, within which time scales quickly diverge, yet no thermodynamic transition nor a low temperature glass phase are present.
Anisotropic dipolar glasses at low dipole concentrations have intrigued much attention, as fluctuations beyond mean field become exceedingly important. Using cluster Monte Carlo algorithm we have shown that at all concentrations, however small, a thermodynamic glass phase is present, with the critical temperature being linear in the concentration, in agreement with mean field theory.
More recently we have addressed the question of the existence of a thermodynamic phase in the electron glass system. For systems with short range interactions, adding site disorder destroys the glass phase. For the electron glass, however, onsite disorder drives the glassy phase, introducing a thermodynamic glass phase at low temperature above a threshold disorder. Other questions we recently addressed is the dependence of glass dynamics on interaction and disorder, in dipolar glasses and in the electron glass, near and far from equilibrium.
- J. C. Andresen, H. G. Katzgraber, V. Oganesyan, and M. Schechter, Existence of a Thermodynamic Spin-Glass Phase in the Zero-Concentration Limit of Anisotropic Dipolar Systems. Physical Review X 4, 041016 (2014).
- O. Asban, A. Amir, Y. Imry, and M. Schechter, Effect of interactions and disorder on the relaxation of two-level systems in amorphous solids. Physical Review B 95, 144207 (2017).
- A. Barzegar, J. C. Andresen, M. Schechter, and H. G. Katzgraber, Numerical observation of a glassy phase in the three-dimensional Coulomb glass. Physical Review B 100, 104418 (2019).
- O. Asban, A. L. Burin, A. Shnirman, and M. Schechter, Polaronic effect of a metal layer on variable range hopping. Physical Review B 103, 045129 (2021).
- P. Bhandari, V. Malik, and M. Schechter, Variable range hopping in a nonequilibrium steady state. Physical Review B 108, 024203 (2023).
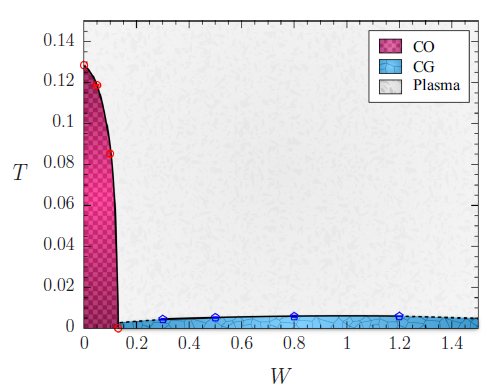
Phase diagram of the electron glass as function of disorder and temperature, from Barzegar et. al., (2019).